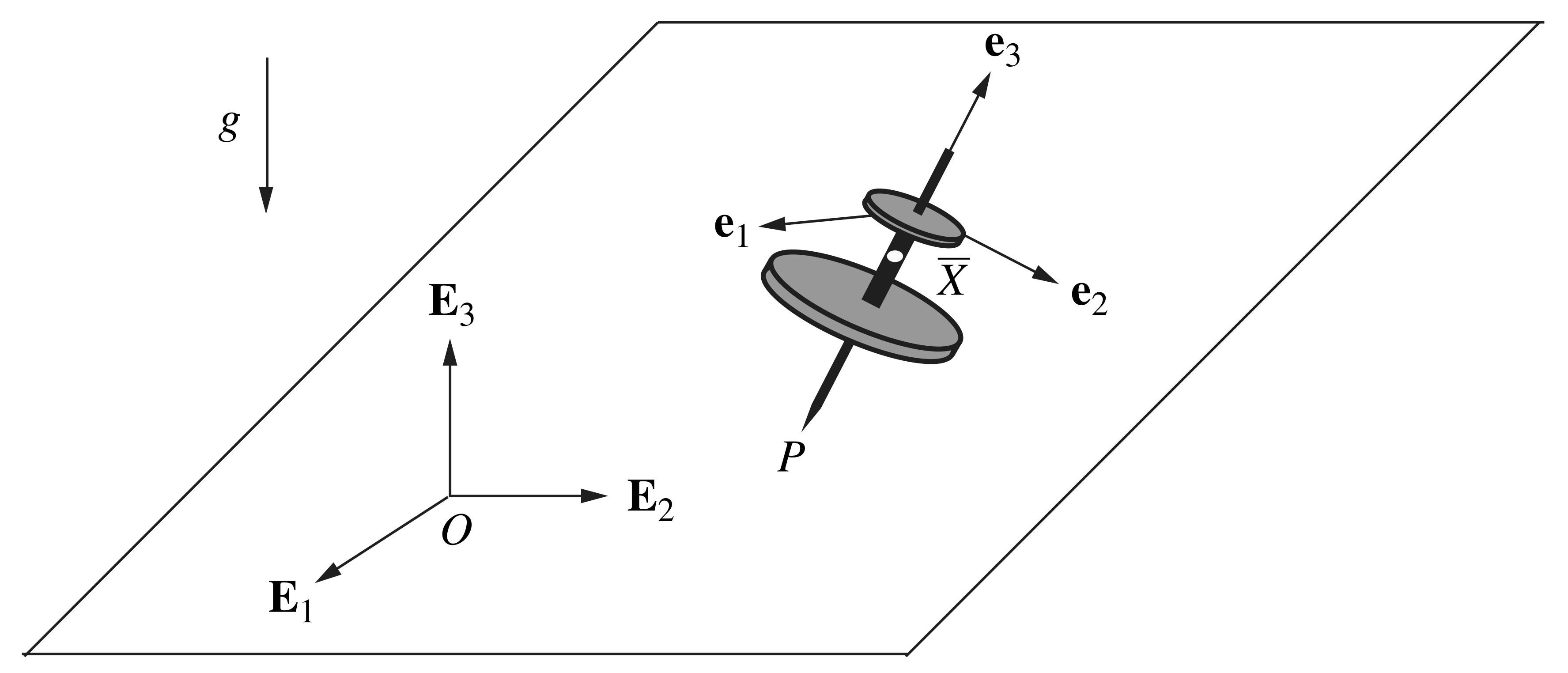
The Poisson top, a close relative to the Lagrange top, is an axisymmetric rigid body that is free to move on a horizontal surface with one point ![]() in contact with the ground, as illustrated in Figure 1 below. In the early 1800s, Poisson [1] examined the dynamics of this top in the (overly optimistic) hopes of being able to use it to establish the vertical (i.e., the plumb line) in a ship at sea.
in contact with the ground, as illustrated in Figure 1 below. In the early 1800s, Poisson [1] examined the dynamics of this top in the (overly optimistic) hopes of being able to use it to establish the vertical (i.e., the plumb line) in a ship at sea.
Contents
Equations of motion
Following our discussion of the Lagrange top, the Poisson top depicted in Figure 1 has mass ![]() , a longitudinal axis of symmetry, and a center of mass
, a longitudinal axis of symmetry, and a center of mass ![]() that falls along this axis such that the top’s principal moments of inertia
that falls along this axis such that the top’s principal moments of inertia ![]() and
and ![]() . The position of the moving contact point
. The position of the moving contact point ![]() relative to the mass center is
relative to the mass center is ![]() , where
, where ![]() is the top’s corotational basis. We locate the top’s center of mass using a set of Cartesian coordinates,
is the top’s corotational basis. We locate the top’s center of mass using a set of Cartesian coordinates, ![]()
![]() , where
, where ![]() denotes the space-fixed basis, while the rotation of the top may be parameterized by a set of Euler angles:
denotes the space-fixed basis, while the rotation of the top may be parameterized by a set of Euler angles: ![]() ,
, ![]() , and
, and ![]() .
.
 .
.In contrast to the Lagrange top, because the Poisson top’s contact point ![]() is able to slide on a horizontal surface, the top is subject to a single integrable (i.e., holonomic) constraint given by
is able to slide on a horizontal surface, the top is subject to a single integrable (i.e., holonomic) constraint given by ![]() ; that is, point
; that is, point ![]() maintains contact with the horizontal surface, and thus it does not have a vertical component of velocity.
maintains contact with the horizontal surface, and thus it does not have a vertical component of velocity.
The equations of motion for the Poisson top may be obtained by a Lagrangian approach, for which the top’s potential energy ![]() , and its total kinetic energy
, and its total kinetic energy ![]() has the form
has the form
(1) ![]()
where ![]() are the corotational components of the top’s angular velocity. In terms of a 3-2-3 set of Euler angles,
are the corotational components of the top’s angular velocity. In terms of a 3-2-3 set of Euler angles, ![]() are related to
are related to ![]() ,
, ![]() , and
, and ![]() and their rates of change according to the following expressions:
and their rates of change according to the following expressions:
(2) 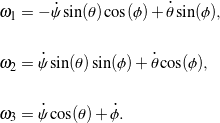
We assume the horizontal surface over which the Poisson top slides is smooth. Upon applying Lagrange’s equations, it can be shown that the top’s equations of motion for the unconstrained coordinates ![]() may be expressed in the second-order matrix-vector form
may be expressed in the second-order matrix-vector form ![]() , where
, where
(3) ![Rendered by QuickLaTeX.com \begin{eqnarray*} && \mathsf{M}(t, \, \mathsf{u}) = \left[ \begin{array}{c c c c c} \lambda_a \cos^2(\theta) + \lambda_t \sin^2(\theta) & 0 & \lambda_a \cos(\theta) & 0 & 0 \\ 0 & \lambda_t + m\ell^2_3\sin^2(\theta) & 0 & 0 & 0 \\ \lambda_a \cos(\theta) & 0 & \lambda_a & 0 & 0 \\ 0 & 0 & 0 & m & 0 \\ 0 & 0 & 0 & 0 & m \\ \end{array} \right], \\ \\ \\ && \upalpha (t, \, \mathsf{u}, \, \dot{\mathsf{u}}) = \left[ \begin{array}{c} 2 \left(\lambda_t - \lambda_a\right) \dot{\psi}\dot{\theta}\cos(\theta)\sin(\theta) - \lambda_a \dot{\phi}\dot{\theta}\sin(\theta) \\ \left(\lambda_a - \lambda_t\right) \dot{\psi}^2\cos(\theta)\sin(\theta) + \lambda_a \dot{\phi}\dot{\psi}\sin(\theta) + m\ell^2_3\dot{\theta}^2\cos(\theta)\sin(\theta) \\ - \lambda_a \dot{\psi}\dot{\theta}\sin(\theta) \\ 0 \\ 0 \\ \end{array} \right], \hspace{1in} \scalebox{0.001}{\textrm{\textcolor{white}{.}}} \\ \\ \\ && \mathsf{f}(t, \, \mathsf{u}) = \left[ \begin{array}{c} 0 \\ m g \ell_3 \sin(\theta) \\ 0 \\ 0 \\ 0 \\ \end{array} \right]. \end{eqnarray*}](https://rotations.berkeley.edu/wp-content/ql-cache/quicklatex.com-d5f4547e405641beeebf10a243dcc8a1_l3.png)
In order to numerically integrate the top’s equations of motion in MATLAB, we introduce the state vector ![]() so that the state-space (i.e., first-order) formulation of the second-order equations of motion is given by
so that the state-space (i.e., first-order) formulation of the second-order equations of motion is given by
(4) ![]()
Simulation and animation
A sample animation of the Poisson top’s motion obtained by numerical simulation is provided in Figure 2. The animation window also displays the evolution of the corotational basis vectors, the trajectory of the top’s contact point ![]() , and the total mechanical energy
, and the total mechanical energy ![]() over time.
over time.
Figure 2. Sample animations of the Poisson top’s motion and the corresponding evolution of the corotational basis vectors, trajectory of the top’s contact point, and energy level over time. The animation was recorded at 8x slower speed.
Note that, as with the Lagrange top, the Poisson top can execute a steady rotational motion with a constant precession rate ![]() , spin rate
, spin rate ![]() , and nutation angle
, and nutation angle ![]() if they satisfy the condition
if they satisfy the condition
(5) ![]()
Indeed, Figure 3 demonstrates one such steady motion. Notice that the path of the top’s contact point ![]() traces out a circle in this case, and this is true of all steady motions.
traces out a circle in this case, and this is true of all steady motions.
Figure 3. Animations of the Poisson top undergoing a steady motion and the corresponding evolution of the corotational basis vectors, trajectory of the top’s contact point, and energy level over time. The animation was recorded at 8x slower speed.
Lastly, we wish to point out that because the top is allowed to slide without friction, its motion conserves not only the total mechanical energy ![]() , but also the lateral components of the top’s linear momentum,
, but also the lateral components of the top’s linear momentum, ![]() and
and ![]() . In addition, the top’s motion conserves two components of the angular momentum with respect to the mass center:
. In addition, the top’s motion conserves two components of the angular momentum with respect to the mass center: ![]() and
and ![]() .
.
Downloads
The MATLAB code used to generate the animations in Figures 2 and 3 is available here. Many thanks to Andreas Hansen for creating this code.