The Poisson top with friction

Here, we present an extension of our previous Poisson top analysis by now assuming the horizontal surface over which the Poisson top slides, as illustrated in Figure 1, is rough. The addition of sliding friction complicates the top’s equations of motion, resulting in fascinating behavior.

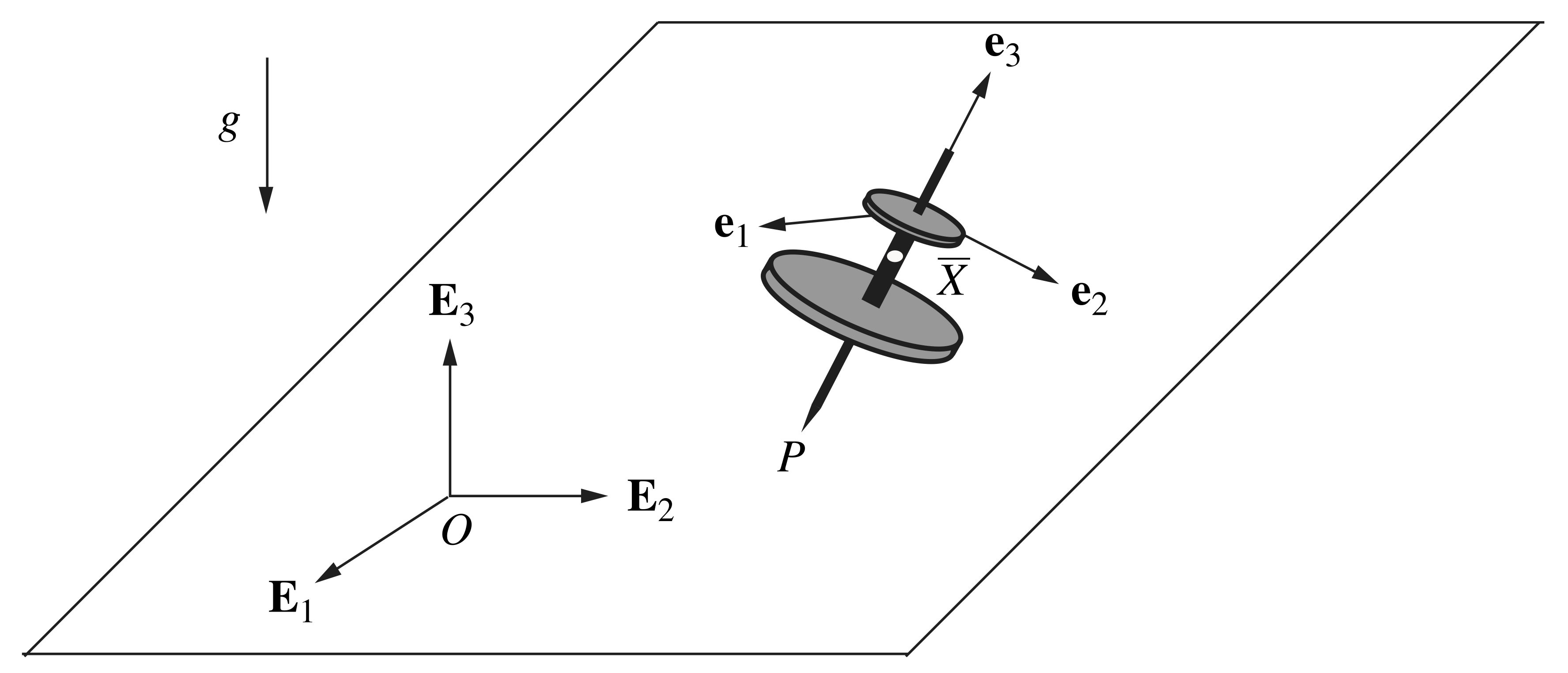
**Figure 1.** Schematic of the Poisson top illustrating the alignment of the corotational basis $\{ \mathbf{e}_{1}, \, \mathbf{e}_{2}, \, \mathbf{e}_{3} \}$ .

**Figure 1.** Schematic of the Poisson top illustrating the alignment of the corotational basis $\{ \mathbf{e}_{1}, \, \mathbf{e}_{2}, \, \mathbf{e}_{3} \}$ .

Contents

Equations of motion

The derivation of the Poisson top’s equations of motion when sliding with friction closely follows the developments presented in our prior friction-free analysis, so we refer the reader to this information and do not repeat the details here. However, we approach the modeling process from a different perspective by deriving the equations of motion via a balance of linear momentum and a balance of angular momentum with respect to the top’s center of mass: $\dot{\mathbf{G}} = \Sigma \mathbf{F}$ and $\dot{\mathbf{H}} = \Sigma \mathbf{M}$ , respectively, where the linear momentum $\mathbf{G} = \sum_{i \, \, = \, 1}^{3} m \dot{x}_{i} \mathbf{E}_{i}$ , and the angular momentum about the mass center of the axisymmetric top is $\mathbf{H} = \lambda_{t} \omega_{1} \mathbf{e}_{1} + \lambda_{t} \omega_{2} \mathbf{e}_{2} + \lambda_{a} \omega_{3} \mathbf{e}_{3}$ . Because the horizontal surface is rough, a sliding friction force $\mathbf{F}_{f}$ acting at the top’s contact point $P$ contributes to the net force $\Sigma \mathbf{F}$ and the net moment $\Sigma \mathbf{M}$ about the mass center:

(1) $\begin{equation*} \mathbf{F}_{f} = - \mu_{\textrm{k}} N \frac{ \mathbf{v}_{P} }{ \Arrowvert \mathbf{v}_{P} \Arrowvert } \ , \end{equation*}$

where $\mu_{\textrm{k}}$ is the coefficient of kinetic friction between the bottom of the top and the surface, $N$ is the vertical normal force exerted on the bottom of the top by the surface, and $\mathbf{v}_{P}$ is the velocity of the contact point. It is important to recall that $\mathbf{v}_{P} \cdot \mathbf{E}_{3} = 0$ . We also depart from our prior work by utilizing a 3-1-3 set of Euler angles to describe the Poisson top’s orientation, in which case the corotational components of angular velocity $\omega_{i}$ are related to the Euler angles $\psi$ , $\theta$ , and $\phi$ and their rates of change as follows:

(2) $\begin{eqnarray*} && \omega_{1} = \dot \psi \sin(\theta) \sin(\phi) + \dot \theta \cos(\phi) , \\ \\ && \omega_{2} = \dot \psi \sin(\theta) \cos(\phi) - \dot \theta \sin(\phi) , \\ \\ && \omega_{3} = \dot \psi \cos(\theta) + \dot \phi . \end{eqnarray*}$

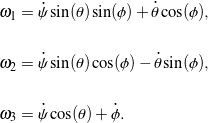
Upon applying the balance laws, it can be shown that the resulting second-order equations of motion may be expressed in the first-order form $\mathsf{M}(t, \, \mathsf{y}) \dot{\mathsf{y}} = \mathsf{f}(t, \, \mathsf{y})$ suitable for numerical integration in MATLAB, where we take the state vector $\mathsf{y} = \left [ \dot{\psi}, \ \dot{\theta}, \ \dot{\phi} , \ \psi, \ \theta, \ \phi, \ \dot{x}_{1}, \ \dot{x}_{2}, \ x_{1}, \ x_{2} \right ]^{T}$ . Owing to the added complexity of sliding friction, the coefficient matrix $\mathsf{M}(t, \, \mathsf{y})$ and the column vector $\mathsf{f}(t, \, \mathsf{y})$ are too expansive to display here.

Simulation and animation

A sample animation of the Poisson top’s simulated motion when acted on by sliding friction is shown in Figure 2. In this simulation, the top is projected along the horizontal surface to demonstrate how friction affects the motion of the contact point. Also, for further contrast with the friction-free case, the initial precession rate, spin rate, and nutation angle are such that they would result in a steady motion of the top when friction is neglected; the loss of mechanical energy is evident in the animated motion.

Figure 2. Animation of the Poisson top’s motion over a rough horizontal surface. The animation was recorded at 4x slower speed.

Clearly, because the top now slides with friction, its motion no longer conserves the total mechanical energy, the lateral components of linear momentum, $\mathbf{G} \cdot \mathbf{E}_{1}$ and $\mathbf{G} \cdot \mathbf{E}_{2}$ , and the vertical component of angular momentum with respect to the mass center, $\mathbf{H} \cdot \mathbf{E}_{3}$ . However, the corotational component of angular momentum $\mathbf{H} \cdot \mathbf{e}_{3}$ is conserved, as the net moment $\Sigma \mathbf{M}$ about the center of mass is always perpendicular to $\mathbf{e}_{3}$ according to our assumption that the mass center falls along the top’s longitudinal axis.

Downloads

The animation in Figure 2 was generated using the following MATLAB code:

Main script:	Solve the Poisson top’s equations of motion
Supporting files:	Derive the Poisson top’s equations of motion ** Animate the Poisson top’s motion

** Run this code first to obtain the symbolic equations of motion called by the main script. (The Symbolic Math Toolbox is required.) This code needs to be run only once, before the first use of the main script.