The Lagrange top | Rotations

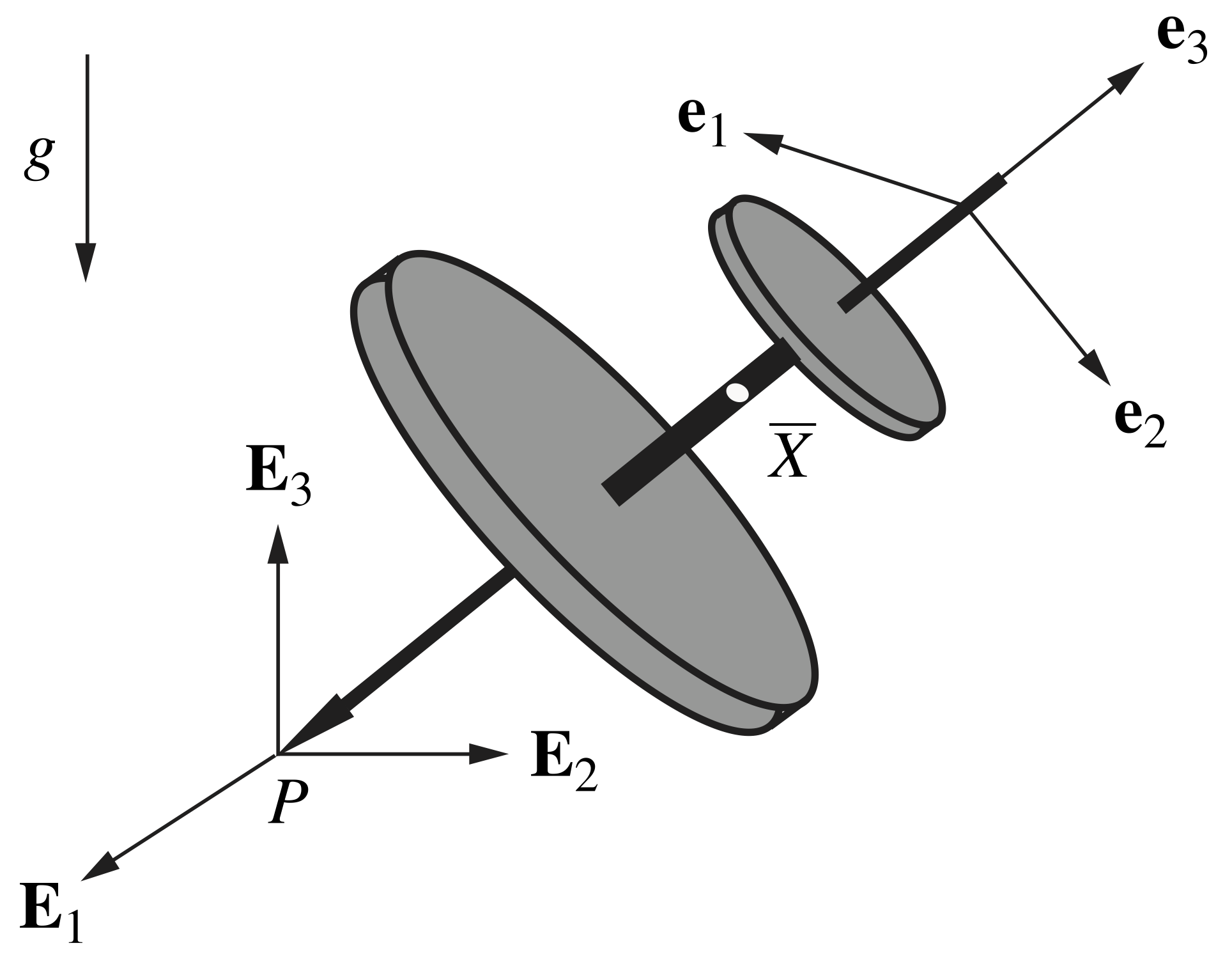
Referring to Figure 1 below, the Lagrange top is an axisymmetric rigid body whose point of contact $P$ with a horizontal surface is fixed. Such an object is referred to as the Lagrange top because Lagrange considered the dynamics of this body in his Mécanique Analytique (see [1]).

Contents

Equations of motion

For the Lagrange top illustrated in Figure 1, we take its mass to be $m$ and assume the fixed contact point $P$ is directly beneath the top’s mass center $\overline{X}$ such that the relative position vector for $P$ is $\bpi_{P} = - \ell_{3} \mathbf{e}_{3}$ , where $\{ \mathbf{e}_{1}, \, \mathbf{e}_{2}, \, \mathbf{e}_{3} \}$ is the top’s corotational basis. We may track the location of the top’s mass center using a set of Cartesian coordinates, $x_{i} = \overline{\mathbf{x}} \cdot \mathbf{E}_{i}$ $(i = 1, \, 2, \, 3)$ , and therefore the linear momentum of the top is given by $\mathbf{G} = \sum_{i \, \, = \, 1}^{3} m \dot{x}_{i} \mathbf{E}_{i}$ , where $\{ \mathbf{E}_{1}, \, \mathbf{E}_{2}, \, \mathbf{E}_{3} \}$ represents the space-fixed basis. The orientation of the top may be described by, say, a 3-1-3 set of Euler angles: $\psi$ , $\theta$ , and $\phi$ .

**Figure 1.** Schematic of the Lagrange top illustrating the alignment of the corotational basis $\{ \mathbf{e}_{1}, \, \mathbf{e}_{2}, \, \mathbf{e}_{3} \}$ .

**Figure 1.** Schematic of the Lagrange top illustrating the alignment of the corotational basis $\{ \mathbf{e}_{1}, \, \mathbf{e}_{2}, \, \mathbf{e}_{3} \}$ .

The Lagrange top’s longitudinal axis is assumed to be an axis of symmetry (i.e., the body is symmetric about the $\mathbf{e}_{3}$ direction), and thus the top’s principal moments of inertia $\lambda_{1} = \lambda_{2} = \lambda_{t}$ and $\lambda_{3} = \lambda_{a}$ . We may then express the angular momentum of the top about its center of mass as $\mathbf{H} = \lambda_{t} \omega_{1} \mathbf{e}_{1} + \lambda_{t} \omega_{2} \mathbf{e}_{2} + \lambda_{a} \omega_{3} \mathbf{e}_{3}$ , where $\omega_{i} = \bomega \cdot \mathbf{e}_{i}$ are the corotational components of angular velocity that, for a 3-1-3 set of Euler angles, are related to $\psi$ , $\theta$ , and $\phi$ and their rates of change as follows:

(1) $\begin{eqnarray*} && \omega_{1} = \dot \psi \sin(\theta) \sin(\phi) + \dot \theta \cos(\phi) , \\ \\ && \omega_{2} = \dot \psi \sin(\theta) \cos(\phi) - \dot \theta \sin(\phi) , \\ \\ && \omega_{3} = \dot \psi \cos(\theta) + \dot \phi . \end{eqnarray*}$

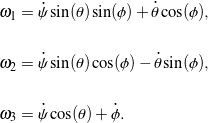
The Lagrange top is subject to three integrable (holonomic) constraints of the form $\mathbf{v}_{P} \cdot \mathbf{E}_{i} = 0$ that arise from the fact that the contact point $P$ is fixed, i.e., the velocity $\mathbf{v}_{P} = \mathbf{0}$ . These constraints relate the location of the mass center to the top’s orientation.

The equations of motion for the Lagrange top may be obtained by applying a balance of linear momentum and a balance of angular momentum with respect to the top’s center of mass: $\dot{\mathbf{G}} = \Sigma \mathbf{F}$ and $\dot{\mathbf{H}} = \Sigma \mathbf{M}$ , respectively, where the top’s weight and the reaction forces at the fixed contact point $P$ contribute to the net force $\Sigma \mathbf{F}$ and the net moment $\Sigma \mathbf{M}$ about the mass center. The resulting differential equations from applying the balance laws can then be expressed in the first-order form $\mathsf{M}(t, \, \mathsf{y}) \dot{\mathsf{y}} = \mathsf{f}(t, \, \mathsf{y})$ for numerical integration in MATLAB, where we define the state vector $\mathsf{y} = \left [ \dot{\psi}, \ \dot{\theta}, \ \dot{\phi} , \ \psi, \ \theta, \ \phi \right ]^{T}$ :

(2) $\begin{eqnarray*} && \mathsf{M}(t, \, \mathsf{y}) = \left[ \begin{array}{c c c c c c} (\lambda_{t} + m \ell_{3}^2) \sin(\theta) & 0 & 0 & 0 & 0 & 0 \\ 0 & \lambda_{t} + m \ell_{3}^2 & 0 & 0 & 0 & 0 \\ \cos(\theta) & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \end{array} \right], \\ \\ \\ && \mathsf{f}(t, \, \mathsf{y}) = \left[ \begin{array}{c} (\lambda_{a} - 2(\lambda_{t} + m \ell_{3}^2) ) \dot{\psi} \dot{\theta} \cos(\theta) + \lambda_{a} \dot{\theta} \dot{\phi} \\ (\lambda_{t} - \lambda_{a} + m \ell_{3}^2) \dot{\psi}^2 \sin(\theta) \cos(\theta) - \lambda_{a} \dot{\psi} \dot{\phi} \sin(\theta) + m g \ell_{3} \sin(\theta) \\ \dot{\psi} \dot{\theta} \sin(\theta) \\ \dot{\psi} \\ \dot{\theta} \\ \dot{\phi} \\ \end{array} \right]. \hspace{1in} \scalebox{0.001}{\textrm{\textcolor{white}{.}}} \end{eqnarray*}$

Simulation and animation

For an arbitrary choice of initial conditions for the Euler angles and their rates of change, numerical simulation shows that the Lagrange top generally behaves like a spherical pendulum, assuming the top is allowed to fall below the horizontal. A typical example of this pendulum-like behavior is animated in Figure 2.

Figure 2. Animation of the pendulum-like behavior of the Lagrange top that is typical for an arbitrary choice of initial conditions. The path of the top’s tip is traced out to illustrate the top’s range of motion. The animation was recorded at 5x slower speed.

However, it is possible for the Lagrange top to undergo a steady motion in which it precesses and spins at constant rates (that is, $\dot{\psi} = \dot{\psi}_{0}$ and $\dot{\phi} = \dot{\phi}_{0}$ , respectively, are constant) while at a fixed nutation angle $\theta_{0}$ under the following condition:

(3) $\begin{equation*} (\lambda_{t} - \lambda_{a} + m \ell_{3}^2) \dot{\psi}_{0}^2 \cos(\theta_{0}) - \lambda_{a} \dot{\psi}_{0} \dot{\phi}_{0} + m g \ell_{3} = 0 . \end{equation*}$

An animation of a representative steady motion is shown in Figure 3.

Figure 3. Animation of the Lagrange top undergoing a steady motion in which the trajectory of the top’s tip is a circle. The animation was recorded at 5x slower speed.

The Lagrange top features several conservations. It can be shown that the top’s simulated motion conserves two components of the top’s angular momentum with respect to the fixed contact point $P$ : $\mathbf{H}_{P} \cdot \mathbf{E}_{3} = \textrm{constant}$ and $\mathbf{H}_{P} \cdot \mathbf{e}_{3} = \textrm{constant}$ . In addition, the top’s total mechanical energy $E$ is conserved:

(4) $\begin{equation*} E = \frac{m}{2} \sum_{i \, \, = \, 1}^{3} \dot{x}_{i}^2 + \frac{1}{2} \left ( \lambda_{t} \omega_{1}^2 + \lambda_{t} \omega_{2}^2 + \lambda_{a} \omega_{3}^2 \right ) + m g x_{3} = \textrm{constant} . \end{equation*}$

Downloads

The animations in Figures 2 and 3 were generated using the following MATLAB code:

Main script:	Solve the Lagrange top’s equations of motion
Supporting files:	Derive the Lagrange top’s equations of motion ** Animate the Lagrange top’s motion

** Run this code first to obtain the symbolic equations of motion called by the main script. (The Symbolic Math Toolbox is required.) This code needs to be run only once, before the first use of the main script.

References

Lagrange, J. L., Mécanique Analytique, in: J.-A. Serret, G. Darboux (eds.), Joseph Louis de Lagrange Oeuvres, Vol. 11/12, 4th ed., Georg Olms Verlag, Heidelberg (1973).