A common source of confusion and error when dealing with different representations of rotations is to inadvertently juxtapose matrix and tensor notations. The resulting error can be further compounded when implementing rotations in computing environments such as MATLAB or Mathematica. Here, we attempt to clear up the source of this confusion. Our main point of emphasis is as follows. Given a rotation, we can use a matrix representation and express the rotation in terms of a matrix ![]() . Alternatively, we can represent the rotation using a rotation tensor
. Alternatively, we can represent the rotation using a rotation tensor ![]() . We show that the components of these two quantities are related by
. We show that the components of these two quantities are related by
(1) ![Rendered by QuickLaTeX.com \begin{equation*} \left[ \begin{array}{c c c} R_{11} & R_{12} & R_{13} \\ R_{21} & R_{22} & R_{23} \\ R_{31} & R_{32} & R_{33} \end{array} \right] = \left[ \begin{array}{c c c} Q_{11} & Q_{12} & Q_{13} \\ Q_{21} & Q_{22} & Q_{23} \\ Q_{31} & Q_{32} & Q_{33} \end{array} \right]^T. \end{equation*}](https://rotations.berkeley.edu/wp-content/ql-cache/quicklatex.com-32be6f42b985b7e785ae2f106a47cfd5_l3.png)
We also address this correspondence in MATLAB implementations of rotations and discuss compound rotations. Because matrix representations of rotations commonly feature in computer codes, our remarks pertaining to compound rotations are also relevant to codes.
Contents
Rotation tensors and their equivalent rotation matrices
Consider a counterclockwise rotation through an angle ![]() about an axis
about an axis ![]() that transforms the set of right-handed basis vectors
that transforms the set of right-handed basis vectors ![]() into a new set of basis vectors
into a new set of basis vectors ![]() . The transformation between the two bases is achieved by a rotation matrix
. The transformation between the two bases is achieved by a rotation matrix ![]() and can be expressed in the following manners:
and can be expressed in the following manners:
(2) ![Rendered by QuickLaTeX.com \begin{equation*} \left[ \begin{array} {c} {\bf t}_1 \\ {\bf t}_2 \\ {\bf t}_3 \end{array} \right] = \left[ \begin{array}{c c c} \cos(\theta) & \sin(\theta) & 0 \\ -\sin(\theta) & \cos(\theta) & 0 \\ 0 & 0 & 1 \end{array} \right] \left[ \begin{array}{c} {\bf p}_1 \\ {\bf p}_2 \\ {\bf p}_3 \end{array} \right] = \left[ \begin{array}{c c c} R_{11} & R_{12} & R_{13} \\ R_{21} & R_{22} & R_{23} \\ R_{31} & R_{32} & R_{33} \end{array} \right] \left[ \begin{array}{c} {\bf p}_1 \\ {\bf p}_2 \\ {\bf p}_3 \end{array} \right] = \mathsf{R} \left[ \begin{array}{c} {\bf p}_1 \\ {\bf p}_2 \\ {\bf p}_3 \end{array} \right]. \hspace{1in} \scalebox{0.001}{\textrm{\textcolor{white}{.}}} \end{equation*}](https://rotations.berkeley.edu/wp-content/ql-cache/quicklatex.com-581a2460ed080646de36b80fdb7c1478_l3.png)
Notice that if ![]() is negative, then the direction of the rotation becomes clockwise. The corresponding rotation matrix is the transpose of
is negative, then the direction of the rotation becomes clockwise. The corresponding rotation matrix is the transpose of ![]()
![]() , denoted by
, denoted by ![]() . This inverse rotation is also observed when the new basis
. This inverse rotation is also observed when the new basis ![]() is transformed to the original basis
is transformed to the original basis ![]() :
:
(3) ![Rendered by QuickLaTeX.com \begin{equation*} \left[ \begin{array}{c} {\bf p}_1 \\ {\bf p}_2 \\ {\bf p}_3 \end{array} \right] = \mathsf{R}^T \left[ \begin{array}{c} {\bf t}_1 \\ {\bf t}_2 \\ {\bf t}_3 \end{array} \right]. \end{equation*}](https://rotations.berkeley.edu/wp-content/ql-cache/quicklatex.com-d2f331d8c8999395e1b122cc9be2fbee_l3.png)
Extrapolating from the above example, for a transformation corresponding to a rotation through an angle ![]() about an axis
about an axis ![]() , we can express the basis vectors
, we can express the basis vectors ![]() as a linear combination of the vectors forming the basis
as a linear combination of the vectors forming the basis ![]() :
:
(4) ![]()
It is of interest here to compare the representation (4) to the corresponding representation using a rotation tensor. To this end, we consider the same transformation from ![]() to
to ![]() expressed using a rotation tensor
expressed using a rotation tensor ![]() :
:
(5) 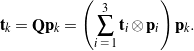
The components ![]() of the rotation tensor
of the rotation tensor ![]() are defined by the representation
are defined by the representation
(6) ![]()
How are the components of the tensor ![]() related to the components of the matrix
related to the components of the matrix ![]() ? To compare and contrast (6) and (4), one can consider a vector
? To compare and contrast (6) and (4), one can consider a vector ![]() acted upon by
acted upon by ![]() . Observing that there are two equivalent representations for the transformation
. Observing that there are two equivalent representations for the transformation ![]() ,
,
(7) 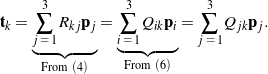
As a result, we can conclude that
(8) ![]()
An alternative method to determine how the tensor components ![]() relate to the matrix components
relate to the matrix components ![]() is to start with (5) and (6) and then invoke (4) as follows:
is to start with (5) and (6) and then invoke (4) as follows:
(9) 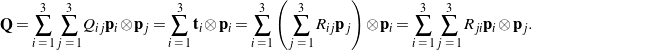
Note the relabeling of the indices in the final representation. Comparing the final representation to the first in (9) yields the conclusion (8). Often, the components ![]() of the rotation tensor
of the rotation tensor ![]() are written in the matrix form
are written in the matrix form ![]() . This matrix is easily confused with the rotation matrix
. This matrix is easily confused with the rotation matrix ![]() . Because the rotation tensor is generally not assumed to be symmetric, this confusion will cause the direction of the rotation to be reversed.
. Because the rotation tensor is generally not assumed to be symmetric, this confusion will cause the direction of the rotation to be reversed.
To illustrate (8), let us return to the example of a rotation about an axis ![]() through an angle
through an angle ![]() . Expressed as a tensor, this rotation has the representation
. Expressed as a tensor, this rotation has the representation
(10) 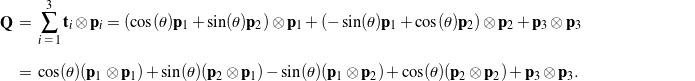
The components of the rotation tensor ![]() expressed as an array
expressed as an array ![]() are readily compared to the components of the corresponding rotation matrix
are readily compared to the components of the corresponding rotation matrix ![]() in (2):
in (2):
(11) ![Rendered by QuickLaTeX.com \begin{equation*} [Q_{ij}] = \left[ \begin{array}{c c c} \cos(\theta) & -\sin(\theta) & 0 \\ \sin(\theta) & \cos(\theta) & 0 \\ 0 & 0 & 1 \end{array} \right] = [R_{ji}] = {\mathsf R}^T. \end{equation*}](https://rotations.berkeley.edu/wp-content/ql-cache/quicklatex.com-28f1995ce922f897b15446d468ccc2d4_l3.png)
As expected, the relationship between the components of ![]() and
and ![]() agrees with (8).
agrees with (8).
MATLAB implementation
One of the most convenient manners to represent vectors in MATLAB is to express them as column vectors. However, the downside of this approach is that we can only write the components of a vector ![]() in just one basis, say,
in just one basis, say, ![]() :
:
(12) ![]()
Consequently, if we wish to express the rotated vector ![]() as a column vector in MATLAB, we must write it in components relative to the basis
as a column vector in MATLAB, we must write it in components relative to the basis ![]() . However, we can take advantage of the tensor representation
. However, we can take advantage of the tensor representation
(13) 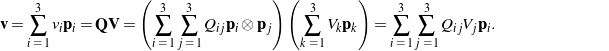
When implemented as a matrix-vector operation,
(14) ![Rendered by QuickLaTeX.com \begin{equation*} \left[ \begin{array}{c} v_1 \\ v_2 \\ v_3 \end{array} \right] = \sum_{j \, \, = \, 1}^{3} \left[ \begin{array}{c} Q_{1j} V_j \\ Q_{2j} V_j \\ Q_{3j} V_j \end{array} \right] = [Q_{ij}] \left[ \begin{array}{c} V_1 \\ V_2 \\ V_3 \end{array} \right] \qquad \longleftrightarrow \qquad \texttt{v = Q*[V1; V2; V3]} , \hspace{1in} \scalebox{0.001}{\textrm{\textcolor{white}{.}}} \end{equation*}](https://rotations.berkeley.edu/wp-content/ql-cache/quicklatex.com-5aba2b635958354ea45289d729a5ad69_l3.png)
where ![]() is a 3
is a 3 ![]() 3 array representing the matrix
3 array representing the matrix ![]() of the components of the rotation tensor
of the components of the rotation tensor ![]() such that
such that ![]() . Again,
. Again, ![]() should not be confused with the corresponding rotation matrix
should not be confused with the corresponding rotation matrix ![]() .
.
Compound rotations
Consider the following sequence of rotations associated with a 3-2-1 set of Euler angles: ![]() through
through ![]() about
about ![]() , then
, then ![]() through
through ![]() about
about ![]() , and lastly
, and lastly ![]() through
through ![]() about
about ![]() . The rotation matrix
. The rotation matrix ![]() that corresponds to the compound rotation is
that corresponds to the compound rotation is
(15) ![Rendered by QuickLaTeX.com \begin{equation*} \mathsf{R}_c = {\mathsf R}_1 {\mathsf R}_2 {\mathsf R}_3 = \left[ \begin{array}{c c c} 1 & 0 & 0 \\ 0 & \cos(\phi) & \sin(\phi) \\ 0 & -\sin(\phi) & \cos(\phi) \end{array} \right] \left[ \begin{array}{c c c} \cos(\theta) & 0 & -\sin(\theta) \\ 0 & 1 & 0 \\ \sin(\theta) & 0 & \cos(\theta) \end{array} \right] \left[ \begin{array}{c c c} \cos(\psi) & \sin(\psi) & 0 \\ -\sin(\psi) & \cos(\psi) & 0 \\ 0 & 0 & 1 \end{array} \right]. \hspace{1in} \scalebox{0.001}{\textrm{\textcolor{white}{.}}} \end{equation*}](https://rotations.berkeley.edu/wp-content/ql-cache/quicklatex.com-65c89bf7e0e2a165d121e3f462bd5b2f_l3.png)
The order of multiplication for the three matrices is important to note. We know from (8) that the array ![]()
![]() of the components of the associated rotation tensor
of the components of the associated rotation tensor ![]() is related to the rotation matrix
is related to the rotation matrix ![]() as follows:
as follows:
(16) ![]()
Explicitly,
(17) ![Rendered by QuickLaTeX.com \begin{equation*} \left[ \begin{array}{c c c} Q_{c_{11}} & Q_{c_{12}} & Q_{c_{13}} \\ Q_{c_{21}} & Q_{c_{22}} & Q_{c_{23}} \\ Q_{c_{31}} & Q_{c_{32}} & Q_{c_{33}} \end{array} \right] = \left[ \begin{array}{c c c} \cos(\psi) & -\sin(\psi) & 0 \\ \sin(\psi) & \cos(\psi) & 0 \\ 0 & 0 & 1 \end{array} \right] \left[ \begin{array}{c c c} \cos(\theta) & 0 & \sin(\theta) \\ 0 & 1 & 0 \\ -\sin(\theta) & 0 & \cos(\theta) \end{array} \right] \left[ \begin{array}{c c c} 1 & 0 & 0 \\ 0 & \cos(\phi) & -\sin(\phi) \\ 0 & \sin(\phi) & \cos(\phi) \end{array} \right]. \hspace{1in} \scalebox{0.001}{\textrm{\textcolor{white}{.}}} \end{equation*}](https://rotations.berkeley.edu/wp-content/ql-cache/quicklatex.com-5c718fa8cb0b424cc84c4197e9e43cdb_l3.png)
Thus, the compound rotation tensor ![]() can be represented in MATLAB as a 3
can be represented in MATLAB as a 3 ![]() 3 array
3 array ![]() populated with the tensor components
populated with the tensor components ![]() such that
such that ![]() , where
, where ![]() is easily constructed by the matrix multiplication in (17).
is easily constructed by the matrix multiplication in (17).