To discuss some elementary features of rotation tensors, it is convenient to first discuss proper-orthogonal tensors. We then appeal to a theorem by Euler who showed that all rotation tensors are, by definition, proper-orthogonal tensors. The forthcoming discussion will lay the foundations for the possibility of three-parameter representations of rotations and, subsequently, the existence of angular velocity vectors. It is also a starting point for several investigations on experimental measurements of rotations.
Contents
Proper-orthogonal tensors
Recall that a proper-orthogonal second-order tensor ![]() is a tensor that has a unit determinant and whose inverse is its transpose:
is a tensor that has a unit determinant and whose inverse is its transpose:
(1) 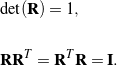
The second of these equations implies that there are six restrictions on the nine components of ![]() . Consequently, only three components of
. Consequently, only three components of ![]() are independent. In other words, any proper-orthogonal tensor can be parameterized by using three independent parameters. Because
are independent. In other words, any proper-orthogonal tensor can be parameterized by using three independent parameters. Because ![]() is a second-order tensor, it has the representation
is a second-order tensor, it has the representation
(2) ![]()
Consider the transformation induced by ![]() on the orthonormal vectors
on the orthonormal vectors ![]() ,
, ![]() , and
, and ![]() that comprise a right-handed basis. We define
that comprise a right-handed basis. We define
(3) ![Rendered by QuickLaTeX.com \begin{eqnarray*} && {\bf t}_1 = {\bf R}{\bf p}_1 = \sum_{i \, \, = \, 1}^3 R_{i1}{\bf p}_i, \\ \\[0.10in] && {\bf t}_2 = {\bf R}{\bf p}_2 = \sum_{i \, \, = \, 1}^3 R_{i2}{\bf p}_i, \\ \\[0.10in] && {\bf t}_3 = {\bf R}{\bf p}_3 = \sum_{i \, \, = \, 1}^3 R_{i3}{\bf p}_i. \end{eqnarray*}](https://rotations.berkeley.edu/wp-content/ql-cache/quicklatex.com-97685a1f4e65237a1a6c0accaa2fc0ec_l3.png)
Notice that by using the vectors ![]() as defined in (3),
as defined in (3), ![]() may also be represented as
may also be represented as
(4) ![]()
We now wish to show that ![]() is also a right-handed orthonormal basis. First, let us verify orthonormality:
is also a right-handed orthonormal basis. First, let us verify orthonormality:
(5) ![]()
Hence, the vectors ![]() are orthonormal. To establish right-handedness, we use the definition of the determinant that features the scalar triple product of three vectors:
are orthonormal. To establish right-handedness, we use the definition of the determinant that features the scalar triple product of three vectors:
(6) ![]()
Therefore, ![]() is a right-handed orthonormal basis. Lastly, after a series of manipulations, we can arrive at another, but rather unusual, representation of the proper-orthogonal tensor
is a right-handed orthonormal basis. Lastly, after a series of manipulations, we can arrive at another, but rather unusual, representation of the proper-orthogonal tensor ![]() :
:
(7) ![Rendered by QuickLaTeX.com \begin{eqnarray*} {\bf R} \!\!\!\!\! &=& \!\!\!\!\! {\bf R}{\bf R}{\bf R}^T = {\bf R} \left(\sum_{i \, \, = \, 1}^3\sum_{k \, \, = \, 1}^3 R_{ik} {\bf p}_i\otimes{\bf p}_k \right) {\bf R}^T = \sum_{i \, \, = \, 1}^3\sum_{k \, \, = \, 1}^3 R_{ik} {\bf R}\left({\bf p}_i\otimes{\bf p}_k\right){\bf R}^T = \sum_{i \, \, = \, 1}^3\sum_{k \, \, = \, 1}^3 R_{ik} \left({\bf R}{\bf p}_i\otimes{\bf R}{\bf p}_k \right) \hspace{1in} \scalebox{0.001}{\textrm{\textcolor{white}{.}}} \\ \\[0.05in] &=& \!\!\!\!\! \sum_{i \, \, = \, 1}^3\sum_{k \, \, = \, 1}^3 R_{ik} {\bf t}_i\otimes{\bf t}_k. \end{eqnarray*}](https://rotations.berkeley.edu/wp-content/ql-cache/quicklatex.com-7353ea6690aad2501f46599a515d4d2a_l3.png)
In summary, we have the following representations for ![]() :
:
(8) ![Rendered by QuickLaTeX.com \begin{eqnarray*} {\bf R} \!\!\!\!\! &=& \!\!\!\!\! \sum_{i \, \, = \, 1}^3\sum_{k \, \, = \, 1}^3 R_{ik} {\bf p}_i\otimes{\bf p}_k \\ \\[0.05in] &=& \!\!\!\!\! \sum_{i \, \, = \, 1}^3\sum_{k \, \, = \, 1}^3 R_{ik} {\bf t}_i\otimes{\bf t}_k \\ \\[0.05in] &=& \!\!\!\!\! \sum_{i \, \, = \, 1}^3 {\bf t}_i\otimes{\bf p}_i. \end{eqnarray*}](https://rotations.berkeley.edu/wp-content/ql-cache/quicklatex.com-a76ed4eac59fc000096c9c546dc4995d_l3.png)
Notice that the components of ![]() for the first two representations are identical, and the handedness of
for the first two representations are identical, and the handedness of ![]() is transferred without change by
is transferred without change by ![]() to
to ![]() . Also observe that the components
. Also observe that the components ![]() of
of ![]() are equal to
are equal to ![]() . As this product is equal to the cosine of the angle between
. As this product is equal to the cosine of the angle between ![]() and
and ![]() , each
, each ![]() is often referred to as a direction cosine. Consequently, the matrix
is often referred to as a direction cosine. Consequently, the matrix ![]() is known as the direction cosine matrix. Clearly, the nine angles whose cosines are
is known as the direction cosine matrix. Clearly, the nine angles whose cosines are ![]() are not all independent, for if they were, then
are not all independent, for if they were, then ![]() would have nine independent components, which would contradict the requirement
would have nine independent components, which would contradict the requirement ![]() . Indeed, as we shall see shortly, it is possible to arrive at three independent angles to parameterize
. Indeed, as we shall see shortly, it is possible to arrive at three independent angles to parameterize ![]() , but these angles are not all easily related to the angles between
, but these angles are not all easily related to the angles between ![]() and
and ![]() .
.
Derivatives of a proper-orthogonal tensor and angular velocity vectors
Consider a proper-orthogonal tensor ![]() that is a function of time:
that is a function of time: ![]() . By the product rule, the time derivative of
. By the product rule, the time derivative of ![]() is
is
(9) ![]()
Because ![]() , the right-hand side of (9) is zero, and thus
, the right-hand side of (9) is zero, and thus
(10) ![]()
In other words, the second-order tensor ![]() is skew-symmetric. For convenience, we define
is skew-symmetric. For convenience, we define
(11) ![]()
in part because this tensor, known as the angular velocity tensor of ![]() , appears in numerous places later on. The skew-symmetry of
, appears in numerous places later on. The skew-symmetry of ![]() allows us to define an associated angular velocity vector
allows us to define an associated angular velocity vector ![]() :
:
(12) ![]()
where ![]() for any vector
for any vector ![]() . A common example of the calculation of an axial vector arises when we consider the motion of a rigid body rotating about the
. A common example of the calculation of an axial vector arises when we consider the motion of a rigid body rotating about the ![]() direction. In this case, the skew-symmetric angular velocity tensor
direction. In this case, the skew-symmetric angular velocity tensor
(13) ![]()
Consequently,
(14) ![]()
and hence we conclude that the axial vector of ![]() is the angular velocity vector
is the angular velocity vector ![]() . It is also useful to verify that
. It is also useful to verify that
(15) ![]()
for any vector ![]() .
.
In a similar manner, we can also show that ![]() is a skew-symmetric tensor and define an angular velocity tensor
is a skew-symmetric tensor and define an angular velocity tensor ![]() with corresponding angular velocity vector
with corresponding angular velocity vector ![]() :
:
(16) ![Rendered by QuickLaTeX.com \begin{eqnarray*} && {\bOmega}_{0_{\bf R}} = {\bf R}^T\dot{\bf R}, \\ \\ && {\bomega}_{0_{\bf R}} = - \frac{1}{2} {\bepsilon}\left[{\bf R}^T \dot{\bf R}\right]. \end{eqnarray*}](https://rotations.berkeley.edu/wp-content/ql-cache/quicklatex.com-08a1f4aa7eccc5b4a1c1b2acd5b6cf95_l3.png)
With the help of the identity
(17) ![]()
which holds for all orthogonal ![]() and all second-order tensors
and all second-order tensors ![]() , it is possible to show that
, it is possible to show that
(18) 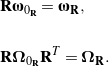
Notice how identity (17) simplifies when ![]() is a proper-orthogonal tensor.
is a proper-orthogonal tensor.
On a final note, if we utilize the representation
(19) ![]()
and take ![]() to be a fixed basis, then
to be a fixed basis, then
(20) ![Rendered by QuickLaTeX.com \begin{eqnarray*} {\bOmega}_{{\bf R}} \!\!\!\!\! &=& \!\!\!\!\! \dot{\bf R}{\bf R}^T = \left(\sum_{i \, \, = \, 1}^3 \dot{\bf t}_i\otimes{\bf p}_i + \sum_{i \, \, = \, 1}^3 {\bf t}_i\otimes{\dot{\bf p}_i} \right){\bf R}^T = \left(\sum_{i \, \, = \, 1}^3 \dot{\bf t}_i\otimes{\bf p}_i\right){\bf R}^T \hspace{1in} \scalebox{0.001}{\textrm{\textcolor{white}{.}}} \\ \\[0.05in] &=& \!\!\!\!\! \sum_{i \, \, = \, 1}^3 \dot{\bf t}_i\otimes{\bf t}_i. \end{eqnarray*}](https://rotations.berkeley.edu/wp-content/ql-cache/quicklatex.com-07dd80397fd725260e5e5c214139a596_l3.png)
Consequently, we find a familiar result:
(21) ![]()
That is, if ![]() are defined by use of a proper-orthogonal tensor
are defined by use of a proper-orthogonal tensor ![]() and a fixed basis
and a fixed basis ![]() , then their time derivatives can be expressed in terms of the angular velocity vector of the rotation tensor and the basis vectors
, then their time derivatives can be expressed in terms of the angular velocity vector of the rotation tensor and the basis vectors ![]() .
.
Corotational derivatives
Consider the following representations of a vector ![]() and a second-order tensor
and a second-order tensor ![]() :
:
(22) 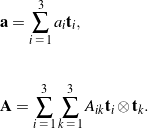
If we assume that ![]() and
and ![]() are functions of time, then
are functions of time, then
(23) ![Rendered by QuickLaTeX.com \begin{eqnarray*} \dot{\bf a} \!\!\!\!\! &=& \!\!\!\!\! \sum_{i \, \, = \, 1}^3 \dot{a}_i {\bf t}_i + \sum_{i \, \, = \, 1}^3 a_i \dot{\bf t}_i = \sum_{i \, \, = \, 1}^3 \dot{a}_i {\bf t}_i + \sum_{i \, \, = \, 1}^3 a_i ({\bomega}_{{\bf R}}\times{\bf t}_i) = \sum_{i \, \, = \, 1}^3 \dot{a}_i {\bf t}_i + {\bomega}_{{\bf R}}\times \left ( \sum_{i \, \, = \, 1}^3 a_i {\bf t}_i \right ) \hspace{1in} \scalebox{0.001}{\textrm{\textcolor{white}{.}}} \\ \\[0.05in] \!\!\!\!\! &=& \!\!\!\!\! \sum_{i \, \, = \, 1}^3 \dot{a}_i {\bf t}_i + {\bomega}_{{\bf R}}\times{\bf a} \end{eqnarray*}](https://rotations.berkeley.edu/wp-content/ql-cache/quicklatex.com-2524c378f6bf3e0c248ca0d4d0572286_l3.png)
and
(24) ![Rendered by QuickLaTeX.com \begin{eqnarray*} \dot{\bf A} \!\!\!\!\! &=& \!\!\!\!\! \sum_{i \, \, = \, 1}^3\sum_{k \, \, = \, 1}^3 \dot{A}_{ik} {\bf t}_i\otimes{\bf t}_k + \sum_{i \, \, = \, 1}^3\sum_{k \, \, = \, 1}^3 A_{ik} \dot{\bf t}_i\otimes{\bf t}_k + \sum_{i \, \, = \, 1}^3\sum_{k \, \, = \, 1}^3 A_{ik} {\bf t}_i\otimes\dot{\bf t}_k \\ \\[0.05in] &=& \!\!\!\!\! \sum_{i \, \, = \, 1}^3\sum_{k \, \, = \, 1}^3 \dot{A}_{ik} {\bf t}_i\otimes{\bf t}_k + \sum_{i \, \, = \, 1}^3\sum_{k \, \, = \, 1}^3 A_{ik} ({\bOmega}_{{\bf R}}{\bf t}_i)\otimes{\bf t}_k + \sum_{i \, \, = \, 1}^3\sum_{k \, \, = \, 1}^3 A_{ik} {\bf t}_i\otimes({\bOmega}_{{\bf R}}{\bf t}_k) \hspace{1in} \scalebox{0.001}{\textrm{\textcolor{white}{.}}} \\ \\[0.05in] &=& \!\!\!\!\! \sum_{i \, \, = \, 1}^3\sum_{k \, \, = \, 1}^3 \dot{A}_{ik} {\bf t}_i\otimes{\bf t}_k + {\bOmega}_{{\bf R}}{\bf A} - {\bf A}{\bOmega}_{{\bf R}}. \end{eqnarray*}](https://rotations.berkeley.edu/wp-content/ql-cache/quicklatex.com-41c7e09c49cf97074dc47ed77304470a_l3.png)
Let ![]() and
and ![]() denote the corotational derivatives (with respect to
denote the corotational derivatives (with respect to ![]() ) of
) of ![]() and
and ![]() , respectively:
, respectively:
(25) 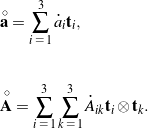
Simply put, ![]() and
and ![]() are the respective derivatives of
are the respective derivatives of ![]() and
and ![]() if the vectors
if the vectors ![]() are constant. With this notation, (23) and (24) simplify to
are constant. With this notation, (23) and (24) simplify to
(26) 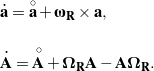
The terms in these expressions involving the angular velocity vector ![]() and the angular velocity tensor
and the angular velocity tensor ![]() are the result of the orthonormal vectors
are the result of the orthonormal vectors ![]() changing with time. Corotational derivatives of vectors and tensors feature prominently in our discussions of relative rotations and the kinematics of rigid bodies.
changing with time. Corotational derivatives of vectors and tensors feature prominently in our discussions of relative rotations and the kinematics of rigid bodies.