It is common practice to use matrices to represent transformations of a vector into another vector. Here, we discuss another quantity, known as a tensor, that achieves the same purpose. We generally denote tensors by uppercase boldfaced symbols, such as ![]() , and symbolize the transformation of a vector
, and symbolize the transformation of a vector ![]() by
by ![]() to a vector
to a vector ![]() as
as
(1) ![]()
The advantages of using tensors are that they are often far more compact than matrices, they are easier to differentiate, and their components transform transparently under changes of bases. The latter feature is very useful when interpreting results in rigid-body kinematics. Consequently, we choose to employ a tensor notation throughout this site for many of the developments we present. This page is intended as both a brief introduction to and review of tensors and their properties. The material provided in the forthcoming sections is standard background for courses in continuum mechanics, and, as such, the primary sources of this information are works by Casey [1, 2], Chadwick [3], and Gurtin [4].
Contents
Preliminaries
To lay the foundation for our upcoming exposition on tensors, we begin with a brief discussion of basis vectors and define two symbols that prove useful in subsequent sections.
Basis vectors
Euclidean three-space is denoted by ![]() . For this space, we define a fixed, right-handed orthonormal basis
. For this space, we define a fixed, right-handed orthonormal basis ![]() . By orthonormal, we mean that for any set of vectors
. By orthonormal, we mean that for any set of vectors ![]() , the dot products
, the dot products ![]() when
when ![]() and
and ![]() when
when ![]() . Unless indicated otherwise, lowercase italic Latin indices such as
. Unless indicated otherwise, lowercase italic Latin indices such as ![]() ,
, ![]() , and
, and ![]() range from 1 to 3. If
range from 1 to 3. If ![]() is right-handed, then the following scalar triple product is positive:
is right-handed, then the following scalar triple product is positive:
(2) ![]()
We also make use of another right-handed orthonormal basis, ![]() , that is not necessarily fixed.
, that is not necessarily fixed.
The Kronecker delta
We use copious amounts of dot products, so it is convenient to define the Kronecker delta ![]() :
:
(3) ![Rendered by QuickLaTeX.com \begin{equation*}\delta_{ij} =\left\{ \begin{array}{c}1 \quad i = j,\\[0.075in]0 \quad i \ne j.\end{array}\right. \end{equation*}](https://rotations.berkeley.edu/wp-content/ql-cache/quicklatex.com-f34d9904d598f2cbc6c6372de0479d85_l3.png)
Clearly,
(4) ![]()
The alternating symbol
We also occasionally make use of the alternating (or Levi-Civita) symbol ![]() , which is defined such that
, which is defined such that
(5) 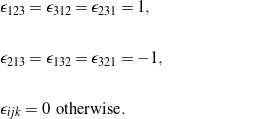
In words, ![]() if
if ![]() is an even permutation of 1, 2, and 3;
is an even permutation of 1, 2, and 3; ![]() if
if ![]() is an odd permutation of 1, 2, and 3; and
is an odd permutation of 1, 2, and 3; and ![]() if either
if either ![]() ,
, ![]() , or
, or ![]() . We also note that
. We also note that
(6) ![]()
which is simple to verify by using the definition of the scalar triple product.
The tensor product of two vectors
The tensor (or cross-bun) product of any two vectors ![]() and
and ![]() in
in ![]() is defined by
is defined by
(7) ![]()
where ![]() is any vector in
is any vector in ![]() . That is,
. That is, ![]() projects
projects ![]() onto
onto ![]() and multiplies the resulting scalar by
and multiplies the resulting scalar by ![]() . Put another way,
. Put another way, ![]() transforms
transforms ![]() into a vector that is parallel to
into a vector that is parallel to ![]() . A related tensor product is defined as follows:
. A related tensor product is defined as follows:
(8) ![]()
In either case, ![]() performs a linear transformation of
performs a linear transformation of ![]() that it acts on. The tensor product has the following useful properties:
that it acts on. The tensor product has the following useful properties:
(9) 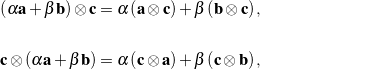
where ![]() and
and ![]() are any two scalars. To prove these identities, one merely shows that the left- and right-hand sides provide the same transformation of any vector
are any two scalars. To prove these identities, one merely shows that the left- and right-hand sides provide the same transformation of any vector ![]() in
in ![]() .
.
Second-order tensors
A second-order tensor ![]() is a linear transformation of
is a linear transformation of ![]() into itself. That is, for any two vectors
into itself. That is, for any two vectors ![]() and
and ![]() and any two scalars
and any two scalars ![]() and
and ![]() ,
,
(10) ![]()
where ![]() and
and ![]() are both vectors in
are both vectors in ![]() . The tensor
. The tensor ![]() is a simple example of a second-order tensor. It is standard to define the following composition rules for second-order tensors:
is a simple example of a second-order tensor. It is standard to define the following composition rules for second-order tensors:
(11) 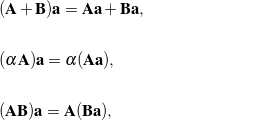
where ![]() and
and ![]() are any second-order tensors. To check if two second-order tensors
are any second-order tensors. To check if two second-order tensors ![]() and
and ![]() are identical, it suffices to show that
are identical, it suffices to show that ![]() for any
for any ![]() . We also define the identity tensor
. We also define the identity tensor ![]() and the zero tensor
and the zero tensor ![]() :
:
(12) 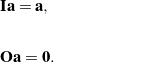
Representations
It is convenient at this stage to establish the following representation for any second-order tensor ![]() :
:
(13) ![]()
where
(14) ![]()
are the components of ![]() relative to the basis
relative to the basis ![]() . The order of the indices
. The order of the indices ![]() and
and ![]() is important. Initially, it is convenient to interpret a tensor using the representation
is important. Initially, it is convenient to interpret a tensor using the representation
(15) ![]()
for which
(16) ![]()
In this light, ![]() transforms
transforms ![]() into
into ![]() . Hence, if we know what
. Hence, if we know what ![]() does to three orthonormal vectors, then we can write its representation immediately. To arrive at representation (13), we examine the action of a second-order tensor
does to three orthonormal vectors, then we can write its representation immediately. To arrive at representation (13), we examine the action of a second-order tensor ![]() on any vector
on any vector ![]() :
:
(17) ![Rendered by QuickLaTeX.com \begin{eqnarray*}{\bf A}{\bf b} \!\!\!\!\! &=& \!\!\!\!\! \sum_{i \, \, = \, 1}^3{\bf A} (b_i {\bf p}_i)= \sum_{i \, \, = \, 1}^3 b_i ({\bf A} {\bf p}_i)= \sum_{i \, \, = \, 1}^3 b_i \left(\sum_{j \, \, = \, 1}^3 A_{ji}{\bf p}_j \right)= \sum_{i \, \, = \, 1}^3 \sum_{j \, \, = \, 1}^3 b_i \left( A_{ji}{\bf p}_j \right)= \left(\sum_{i \, \, = \, 1}^3 \sum_{j \, \, = \, 1}^3 A_{ji}{\bf p}_j\otimes{\bf p}_i \right) \left( \sum_{k \, \, = \, 1}^3 b_k{\bf p}_k \right) \hspace{1in} \scalebox{0.001}{\textrm{\textcolor{white}{.}}}\\\\[0.10in]&=& \!\!\!\!\! \left( \sum_{i \, \, = \, 1}^3 \sum_{j \, \, = \, 1}^3 A_{ji}{\bf p}_j\otimes{\bf p}_i \right) {\bf b} ,\end{eqnarray*}](https://rotations.berkeley.edu/wp-content/ql-cache/quicklatex.com-f3222afa97f0231d7924beb1d03aa2cc_l3.png)
where we used the definition of the tensor product of two vectors in the next-to-last step. Thus, we infer that ![]() has the representation given by (13). We can use this representation to establish expressions for the transformation induced by
has the representation given by (13). We can use this representation to establish expressions for the transformation induced by ![]() . To proceed, define
. To proceed, define ![]() , in which case, from (17),
, in which case, from (17),
(18) ![]()
The components ![]() of
of ![]() are then given by
are then given by
(19) ![]()
When expressed in matrix notation, (19) has a familiar form:
(20) ![Rendered by QuickLaTeX.com \begin{equation*}\left[ \begin{array}{c c c}c_{1} \\c_{2} \\c_{3} \\\end{array} \right] =\left[ \begin{array}{c c c}A_{11} & A_{12} & A_{13} \\A_{21} & A_{22} & A_{23} \\A_{31} & A_{32} & A_{33} \\\end{array} \right]\left[ \begin{array}{c c c}b_{1} \\b_{2} \\b_{3} \\\end{array} \right].\end{equation*}](https://rotations.berkeley.edu/wp-content/ql-cache/quicklatex.com-87cbc6a755ce82900094e4eea458a366_l3.png)
Note that (20) implies that the identity tensor has the representation ![]() .
.
The product of two second-order tensors
We now turn to the product of two second-order tensors ![]() and
and ![]() . The product
. The product ![]() is defined here to be a second-order tensor
is defined here to be a second-order tensor ![]() . First, let
. First, let
(21) 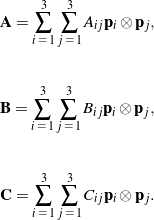
We then solve the equations
(22) ![]()
for the nine components of ![]() , where
, where ![]() is any vector. Using the arbitrariness of
is any vector. Using the arbitrariness of ![]() , we conclude that the components of the three tensors, which are all expressed in the same basis, are related by
, we conclude that the components of the three tensors, which are all expressed in the same basis, are related by
(23) ![]()
This result is identical to that for matrix multiplication. Indeed, if we define three matrices whose components are ![]() ,
, ![]() , and
, and ![]() , then we find the representation
, then we find the representation
(24) ![Rendered by QuickLaTeX.com \begin{equation*}\left[ \begin{array}{c c c }C_{11} & C_{12} & C_{13} \\C_{21} & C_{22} & C_{23} \\C_{31} & C_{32} & C_{33}\end{array} \right] =\left[ \begin{array}{c c c }A_{11} & A_{12} & A_{13} \\A_{21} & A_{22} & A_{23} \\A_{31} & A_{32} & A_{33}\end{array} \right]\left[ \begin{array}{c c c }B_{11} & B_{12} & B_{13} \\B_{21} & B_{22} & B_{23} \\B_{31} & B_{32} & B_{33}\end{array} \right]. \hspace{1in} \scalebox{0.001}{\textrm{\textcolor{white}{.}}}\end{equation*}](https://rotations.berkeley.edu/wp-content/ql-cache/quicklatex.com-bc1366f9bf41c8634bfd32807ca0ed8f_l3.png)
It is straightforward to establish a similar representation for the product ![]() . Finally, consider the product of two second-order tensors
. Finally, consider the product of two second-order tensors ![]() and
and ![]() :
:
(25) ![]()
This result is the simplest way to remember how to multiply two second-order tensors.
Symmetric and skew-symmetric tensors
The transpose ![]() of a second-order tensor
of a second-order tensor ![]() is defined such that
is defined such that
(26) ![]()
for any two vectors ![]() and
and ![]() . If we consider the second-order tensor
. If we consider the second-order tensor ![]() , then we can use definition (26) to show that
, then we can use definition (26) to show that
(27) 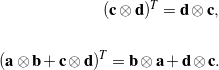
Given any two second-order tensors ![]() and
and ![]() , it can be shown that the transpose
, it can be shown that the transpose ![]() . If
. If ![]() , then
, then ![]() is said to be symmetric. On the other hand,
is said to be symmetric. On the other hand, ![]() is skew-symmetric if
is skew-symmetric if ![]() . Using the representation (13) for
. Using the representation (13) for ![]() and the identity (27)1, we find that the tensor components
and the identity (27)1, we find that the tensor components ![]() when
when ![]() is symmetric and
is symmetric and ![]() when
when ![]() is skew-symmetric. These results imply that
is skew-symmetric. These results imply that ![]() has six independent components when it is symmetric but only three independent components when skew-symmetric. Lastly, it is always possible to decompose any second-order tensor
has six independent components when it is symmetric but only three independent components when skew-symmetric. Lastly, it is always possible to decompose any second-order tensor ![]() into the sum of a symmetric tensor and a skew-symmetric tensor:
into the sum of a symmetric tensor and a skew-symmetric tensor:
(28) 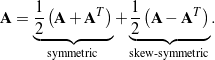
Invariants
There are three scalar quantities associated with a second-order tensor that are independent of the right-handed orthonormal basis used for ![]() . Because these quantities are independent of the basis, they are known as the (principal) invariants of a second-order tensor. Given a second-order tensor
. Because these quantities are independent of the basis, they are known as the (principal) invariants of a second-order tensor. Given a second-order tensor ![]() , the invariants
, the invariants ![]() ,
, ![]() , and
, and ![]() of
of ![]() are defined as
are defined as
(29) ![Rendered by QuickLaTeX.com \begin{eqnarray*}&& I_{\bf A}[{\bf a}, \, {\bf b}, \, {\bf c}] =[{\bf A}{\bf a}, \, {\bf b}, \, {\bf c}] +[{\bf a}, \, {\bf A}{\bf b}, \, {\bf c}] +[{\bf a}, \, {\bf b}, \, {\bf A}{\bf c}] ,\\\\&& II_{\bf A}[{\bf a}, \, {\bf b}, \, {\bf c}] =\mbox{[}{\bf a}, \, {\bf A}{\bf b}, \, {\bf A}{\bf c}] +\mbox{[}{\bf A}{\bf a}, \, {\bf b}, \, {\bf A}{\bf c}] +\mbox{[}{\bf A}{\bf a}, \, {\bf A}{\bf b}, \, {\bf c}] , \\\\&& III_{\bf A}[{\bf a}, \, {\bf b}, \, {\bf c}] =\mbox{[}{\bf A}{\bf a}, \, {\bf A}{\bf b}, \, {\bf A}{\bf c}] ,\end{eqnarray*}](https://rotations.berkeley.edu/wp-content/ql-cache/quicklatex.com-c85ebd453a18ee10b5ff483e5cd65fd2_l3.png)
where ![]() ,
, ![]() , and
, and ![]() are any three vectors. The first invariant
are any three vectors. The first invariant ![]() is known as the trace of a tensor
is known as the trace of a tensor ![]() , and the third invariant
, and the third invariant ![]() is known as the determinant of
is known as the determinant of ![]() :
:
(30) 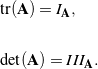
Suppose we represent ![]() in terms of a right-handed orthonormal basis
in terms of a right-handed orthonormal basis ![]() in
in ![]() , such as in representation (13). If we take
, such as in representation (13). If we take ![]() ,
, ![]() , and
, and ![]() , then
, then
(31) ![Rendered by QuickLaTeX.com \begin{eqnarray*}&& [{\bf p}_1, \, {\bf p}_2, \, {\bf p}_3] = 1,\\\\[0.10in]&& \mbox{[}{\bf A}{\bf p}_1, \, {\bf p}_2, \, {\bf p}_3] +[{\bf p}_1, \, {\bf A}{\bf p}_2, \, {\bf p}_3] +[{\bf p}_1, \, {\bf p}_2, \, {\bf A}{\bf p}_3] =\sum_{i \, \, = \, 1}^3 ({\bf A}{\bf p}_i)\cdot{\bf p}_i = A_{11} + A_{22} + A_{33}, \hspace{1in} \scalebox{0.001}{\textrm{\textcolor{white}{.}}}\\\\\\&& \mbox{[}{\bf A}{\bf p}_1, \, {\bf A}{\bf p}_2, \, {\bf A}{\bf p}_3] =\sum_{i \, \, = \, 1}^3 \sum_{j \, \, = \, 1}^3 \sum_{k \, \, = \, 1}^3 \altepsilon_{ijk} A_{i1}A_{j2}A_{k3} =\det \left(\left[ \begin{array}{c c c }A_{11} & A_{12} & A_{13} \\A_{21} & A_{22} & A_{23} \\A_{31} & A_{32} & A_{33}\end{array} \right] \right) .\end{eqnarray*}](https://rotations.berkeley.edu/wp-content/ql-cache/quicklatex.com-6d2a72100de3728ac6d2d426ee4c9bb4_l3.png)
Consequently, the trace of ![]() is given by
is given by
(32) ![]()
A similar result holds for the trace of a matrix. We also note the related result ![]() . In addition, we find that the determinant of
. In addition, we find that the determinant of ![]() can be computed using a familiar matrix representation:
can be computed using a familiar matrix representation:
(33) ![Rendered by QuickLaTeX.com \begin{equation*}\det({\bf A}) =\sum_{i \, \, = \, 1}^3 \sum_{j \, \, = \, 1}^3 \sum_{k \, \, = \, 1}^3 \altepsilon_{ijk} A_{i1}A_{j2}A_{k3} =\det \left(\left[ \begin{array}{c c c }A_{11} & A_{12} & A_{13} \\A_{21} & A_{22} & A_{23} \\A_{31} & A_{32} & A_{33}\end{array} \right]\right). \hspace{1in} \scalebox{0.001}{\textrm{\textcolor{white}{.}}}\end{equation*}](https://rotations.berkeley.edu/wp-content/ql-cache/quicklatex.com-e30637cd321fe1484393a09ccb82ae2f_l3.png)
Inverses and adjugates
The inverse ![]() of a second-order tensor
of a second-order tensor ![]() is the tensor that satisfies
is the tensor that satisfies
(34) ![]()
For the inverse of ![]() to exist, its determinant
to exist, its determinant ![]() . Taking the transpose of (34), we find that the inverse of the transpose of
. Taking the transpose of (34), we find that the inverse of the transpose of ![]() is the transpose of the inverse. The adjugate
is the transpose of the inverse. The adjugate ![]() satisfies
satisfies
(35) ![]()
for any two vectors ![]() and
and ![]() . If
. If ![]() is invertible, then (35) yields a relationship between
is invertible, then (35) yields a relationship between ![]() and
and ![]() :
:
(36) ![]()
Eigenvalues and eigenvectors
The eigenvalues (or characteristic values, or principal values) of a second-order tensor ![]() are defined as the roots
are defined as the roots ![]() of the characteristic equation
of the characteristic equation
(37) ![]()
The three roots of this equation are denoted by ![]() ,
, ![]() , and
, and ![]() . On expanding the characteristic equation (37), we find that
. On expanding the characteristic equation (37), we find that
(38) ![]()
where
(39) ![Rendered by QuickLaTeX.com \begin{eqnarray*}&& I_{\bf A} = \mbox{tr}({\bf A}) = \lambda_1 + \lambda_2 + \lambda_3 ,\\\\[0.15in]&& II_{\bf A} = \frac{1}{2}(\mbox{tr}({\bf A})^2 - \mbox{tr}({\bf A}^2) ) = \lambda_1\lambda_2 + \lambda_2\lambda_3 + \lambda_1\lambda_3 ,\\\\[0.15in]&& III_{\bf A} = \det({\bf A}) = \lambda_1\lambda_2\lambda_3 .\end{eqnarray*}](https://rotations.berkeley.edu/wp-content/ql-cache/quicklatex.com-53b0d7b7983735ede8be3d2e85ba0a8e_l3.png)
The corresponding eigenvectors (or characteristic directions, or principal directions) of ![]() are the vectors
are the vectors ![]() that satisfy
that satisfy
(40) ![]()
A second-order tensor has three eigenvectors, one associated with each eigenvalue. To determine these eigenvectors, we express (40), with the help of (20), in matrix-vector form and then use standard solution techniques from linear algebra. Note that the eigenvectors are unique up to a multiplicative constant.
Proper-orthogonal tensors
A second-order tensor ![]() is said to be orthogonal if
is said to be orthogonal if ![]() . That is, the transpose of an orthogonal tensor is its inverse. It also follows that
. That is, the transpose of an orthogonal tensor is its inverse. It also follows that ![]() . An orthogonal tensor
. An orthogonal tensor ![]() has the unique property that
has the unique property that ![]() for any vector
for any vector ![]() , and so it preserves the length of the vector that it transforms. A tensor
, and so it preserves the length of the vector that it transforms. A tensor ![]() is proper-orthogonal if it is orthogonal and its determinant
is proper-orthogonal if it is orthogonal and its determinant ![]() specifically. Thus, proper-orthogonal second-order tensors are a subclass of the second-order orthogonal tensors.
specifically. Thus, proper-orthogonal second-order tensors are a subclass of the second-order orthogonal tensors.
Positive-definite tensors
A second-order tensor ![]() is said to be positive-definite if
is said to be positive-definite if ![]() for any vector
for any vector ![]() and
and ![]() if, and only if,
if, and only if, ![]() . A consequence of this definition is that a skew-symmetric second-order tensor can never be positive-definite. If
. A consequence of this definition is that a skew-symmetric second-order tensor can never be positive-definite. If ![]() is positive-definite, then all three of its eigenvalues are positive and, furthermore, the tensor has the representation
is positive-definite, then all three of its eigenvalues are positive and, furthermore, the tensor has the representation
(41) ![]()
where ![]() and
and ![]() are the eigenvalues and eigenvectors of
are the eigenvalues and eigenvectors of ![]() , respectively. This representation is often known as the spectral decomposition.
, respectively. This representation is often known as the spectral decomposition.
Third-order tensors
A third-order tensor transforms vectors into second-order tensors and may transform second-order tensors into vectors. With respect to a right-handed orthonormal basis ![]() , any third-order tensor
, any third-order tensor ![]() can be represented as
can be represented as
(42) ![]()
and we define the following two tensor products:
(43) ![Rendered by QuickLaTeX.com \begin{eqnarray*}&& ({\bf a}\otimes{\bf b}\otimes{\bf c})\left[{\bf d}\otimes{\bf e}\right] =({\bf b}\cdot{\bf d})({\bf c}\cdot{\bf e}) {\bf a}, \\\\&& ({\bf a}\otimes{\bf b}\otimes{\bf c}){\bf d} = ({\bf c}\cdot{\bf d}) ({\bf a}\otimes{\bf b}).\end{eqnarray*}](https://rotations.berkeley.edu/wp-content/ql-cache/quicklatex.com-529710423544fb595a660b0f6fc87f13_l3.png)
Note the presence of the brackets ![]() in (43)1. The main example of a third-order tensor we use throughout this site is the alternator
in (43)1. The main example of a third-order tensor we use throughout this site is the alternator ![]() :
:
(44) ![]()
This tensor has some useful features. First, if ![]() is a symmetric second-order tensor, then
is a symmetric second-order tensor, then ![]() . Second, for any vector
. Second, for any vector ![]() ,
,
(45) 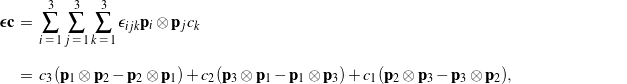
which is a skew-symmetric second-order tensor. Thus, ![]() can be used to transform a vector into a second-order skew-symmetric tensor and transform the skew-symmetric part of a second-order tensor into a vector.
can be used to transform a vector into a second-order skew-symmetric tensor and transform the skew-symmetric part of a second-order tensor into a vector.
Axial vectors
The fact that the third-order alternating tensor ![]() acts on a vector to produce a skew-symmetric second-order tensor enables us to define a skew-symmetric tensor
acts on a vector to produce a skew-symmetric second-order tensor enables us to define a skew-symmetric tensor ![]() for every vector
for every vector ![]() , and vice versa:
, and vice versa:
(46) ![Rendered by QuickLaTeX.com \begin{eqnarray*}&& {\bf C} = - {\bepsilon}{\bf c},\\\\[0.10in]&& {\bf c} = - \frac{1}{2}{\bepsilon}\left[{\bf C}\right]. \end{eqnarray*}](https://rotations.berkeley.edu/wp-content/ql-cache/quicklatex.com-25cfa8afc3c62522795de0b0babbb20e_l3.png)
The vector ![]() is known as the axial vector of
is known as the axial vector of ![]() . Notice that if
. Notice that if ![]() has the representation
has the representation
(47) ![]()
then, with the help of (43)1, its axial vector
(48) ![]()
We also note the important result
(49) ![]()
for any other vector ![]() . This identity allows us to replace cross products with tensor products, and vice versa. We often express the relationship between a skew-symmetric tensor
. This identity allows us to replace cross products with tensor products, and vice versa. We often express the relationship between a skew-symmetric tensor ![]() and its axial vector
and its axial vector ![]() without explicit mention of the alternator
without explicit mention of the alternator ![]() :
:
(50) 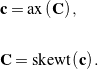
Differentiation of tensors
One often encounters derivatives of tensors. Suppose a second-order tensor ![]() has the representation (13), where the tensor components
has the representation (13), where the tensor components ![]() and the basis vectors
and the basis vectors ![]() are functions of time. The time derivative of
are functions of time. The time derivative of ![]() is defined as
is defined as
(51) ![]()
Notice that we differentiate both the components and the basis vectors. We can also define a chain rule and product rules. If the tensors ![]() and
and ![]() and the vector
and the vector ![]() , then
, then
(52) ![Rendered by QuickLaTeX.com \begin{eqnarray*}&& \dot{\bf A} = \frac{\partial {\bf A}}{\partial q} \dot{q},\\\\[0.10in]&& \dot{ \overline{ {\bf A}{\bf B} } } = \dot{\bf A}{\bf B} + {\bf A}\dot{\bf B}, \\\\&& \dot{ \overline{ {\bf A}{\bf c} } } = \dot{\bf A}{\bf c} + {\bf A}\dot{\bf c}.\end{eqnarray*}](https://rotations.berkeley.edu/wp-content/ql-cache/quicklatex.com-d9ba6ae4f68fc802dd92f8d552199f81_l3.png)
Now, consider a function ![]() . The derivative of this function with respect to
. The derivative of this function with respect to ![]() is defined to be the second-order tensor
is defined to be the second-order tensor
(53) ![]()
In addition, if the basis vectors ![]() are constant, then
are constant, then
(54) ![]()
References
- Casey, J., A treatment of rigid body dynamics, ASME Journal of Applied Mechanics 50(4a) 905–907 and 51 227 (1983).
- Casey, J., On the advantages of a geometrical viewpoint in the derivation of Lagrange’s equations for a rigid continuum, Zeitschrift für angewandte Mathematik und Physik 46 S805–S847 (1995).
- Chadwick, P., Continuum Mechanics: Concise Theory and Problems, Dover Publications, New York (1999). Reprint of the George Allen & Unwin Ltd., London, 1976 edition.
- Gurtin, M. E., An Introduction to Continuum Mechanics, Academic Press, New York (1981).