To motivate many of our later developments, we start with the simplest case of a rotation: a rotation about a fixed axis ![]() through an angle
through an angle ![]() . This example should be familiar to you from many different venues. To describe this rotation, we consider the action of this rotation on the set of fixed, orthonormal, right-handed basis vectors
. This example should be familiar to you from many different venues. To describe this rotation, we consider the action of this rotation on the set of fixed, orthonormal, right-handed basis vectors ![]() . As depicted in Figure 1, we suppose that these vectors are transformed to the set
. As depicted in Figure 1, we suppose that these vectors are transformed to the set ![]() by the rotation.
by the rotation.
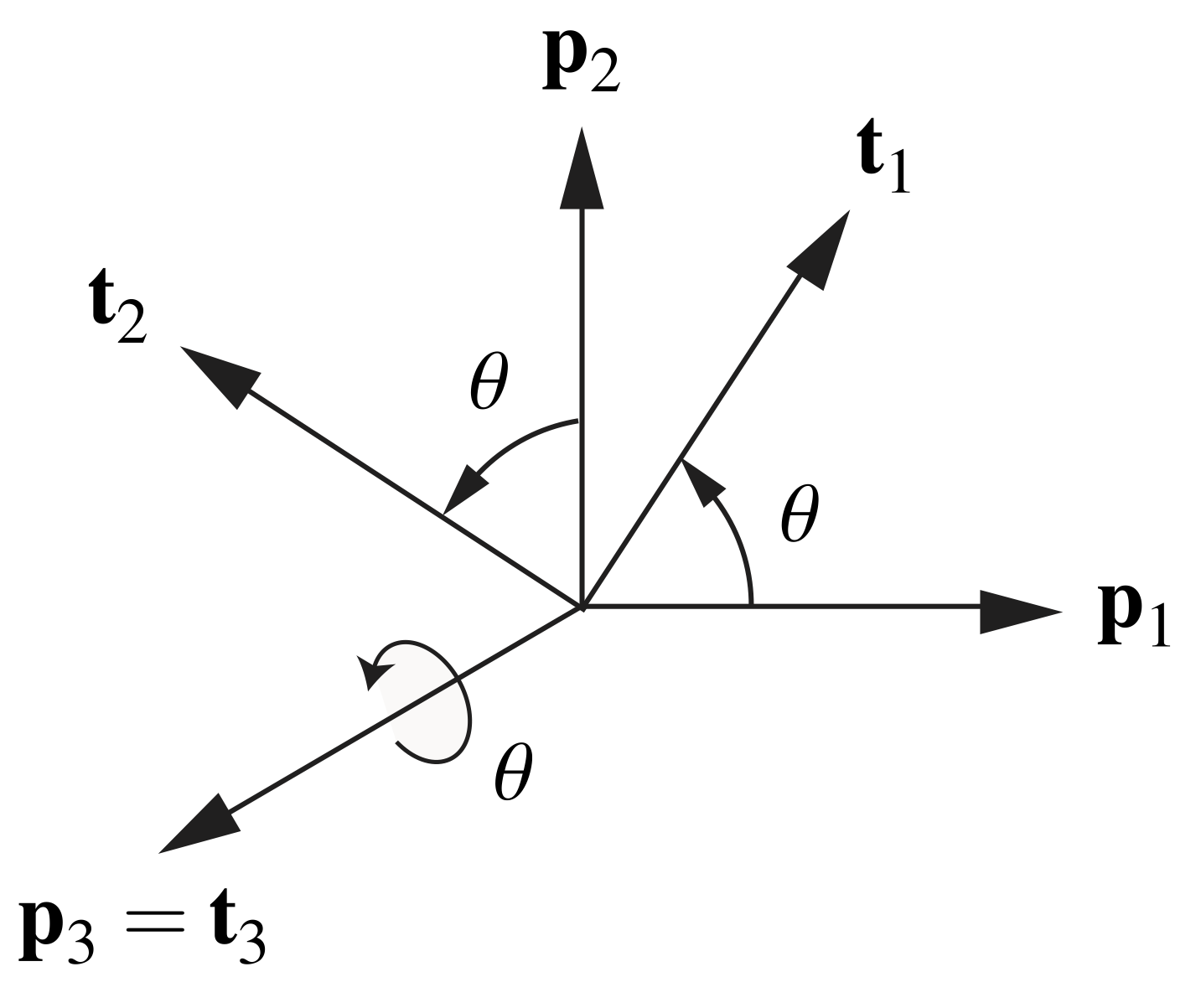
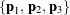 into
into 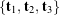 by a rotation about
by a rotation about 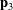 through an angle
through an angle 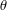 .
.[toc]
A matrix representation of the rotation
Using a matrix notation, we can represent the transformation from the set of basis vectors ![]() to
to ![]() as
as
(1) ![Rendered by QuickLaTeX.com \begin{equation*} \left[ \begin{array}{c} {\bf t}_1 \\ {\bf t}_2 \\ {\bf t}_3 \end{array} \right] = \underbrace{\left[ \begin{array}{c c c } \cos(\theta) & \sin(\theta) & 0 \\ - \sin(\theta) & \cos(\theta) & 0 \\ 0 & 0 & 1 \end{array} \right]}_{\mathsf{R}} \left[\begin{array}{c} {\bf p}_1 \\ {\bf p}_2 \\ {\bf p}_3 \end{array} \right] . \end{equation*}](https://rotations.berkeley.edu/wp-content/ql-cache/quicklatex.com-e9421e5e90d0e38c2a3cdfaa4fa8bf67_l3.png)
It is easy to see that the matrix ![]() in (1) has a unit determinant, and its inverse is its transpose:
in (1) has a unit determinant, and its inverse is its transpose: ![]() . That is, the matrix
. That is, the matrix ![]() is proper-orthogonal. By differentiating (1) with respect to time, we find that
is proper-orthogonal. By differentiating (1) with respect to time, we find that
(2) ![Rendered by QuickLaTeX.com \begin{equation*} \left[ \begin{array}{c} \dot{\bf t}_1 \\ \dot{\bf t}_2 \\ \dot{\bf t}_3 \end{array} \right] = \underbrace{ \dot{\theta} \left[ \begin{array}{c c c } - \sin(\theta) & \cos(\theta) & 0 \\ - \cos(\theta) & - \sin(\theta) & 0 \\ 0 & 0 & 0 \end{array} \right]}_{ \dot{\mathsf{R}} } \left[\begin{array}{c} {\bf p}_1 \\ {\bf p}_2 \\ {\bf p}_3 \end{array} \right]. \end{equation*}](https://rotations.berkeley.edu/wp-content/ql-cache/quicklatex.com-835fcd61aab8db4e4ec5ca18991d3dab_l3.png)
Using the fact that ![]() , we can easily replace
, we can easily replace ![]()
![]() in (2) with
in (2) with ![]() to obtain
to obtain
(3) ![Rendered by QuickLaTeX.com \begin{eqnarray*} \left[ \begin{array}{c} \dot{\bf t}_1 \\ \dot{\bf t}_2 \\ \dot{\bf t}_3 \end{array} \right] \!\!\!\!\! &=& \!\!\!\!\! \underbrace{ \dot{\theta} \left[ \begin{array}{c c c } - \sin(\theta) & \cos(\theta) & 0 \\ - \cos(\theta) & - \sin(\theta) & 0 \\ 0 & 0 & 0 \end{array} \right] }_{ \dot{\mathsf{R}} } \underbrace{ \left[ \begin{array}{c c c } \cos(\theta) & - \sin(\theta) & 0 \\ \sin(\theta) & \cos(\theta) & 0 \\ 0 & 0 & 1 \end{array} \right] }_{ \mathsf{R}^T } \left[\begin{array}{c} {\bf t}_1 \\ {\bf t}_2 \\ {\bf t}_3 \end{array} \right] \hspace{1in} \scalebox{0.001}{\textrm{\textcolor{white}{.}}} \\ \\[0.05in] &=& \!\!\!\!\! \underbrace{\dot{\theta} \left[ \begin{array}{c c c } 0 & 1 & 0 \\ - 1 & 0 & 0 \\ 0 & 0 & 0 \end{array} \right]}_{\dot{\mathsf{R}}\mathsf{R}^T} \left[\begin{array}{c} {\bf t}_1 \\ {\bf t}_2 \\ {\bf t}_3 \end{array} \right]. \end{eqnarray*}](https://rotations.berkeley.edu/wp-content/ql-cache/quicklatex.com-ba36d370170de8679709b7dccfd8ddeb_l3.png)
Notice that this is equivalent to the familiar results ![]() and
and ![]() from cylindrical polar coordinates. It should also be clear from (3) that
from cylindrical polar coordinates. It should also be clear from (3) that ![]() is a skew-symmetric matrix. A vector
is a skew-symmetric matrix. A vector ![]() can be introduced that has the useful property that
can be introduced that has the useful property that
(4) ![]()
You should notice how the vector ![]() can be inferred from the components of
can be inferred from the components of ![]() .
.
A tensor representation of the rotation
It is convenient to use a tensor notation1 to describe the rotation we have been discussing. In particular, we can write (1) in the form
(5) ![]()
where ![]() is the tensor
is the tensor
(6) ![]()
It can be shown that this representation of the rotation is equivalent to (1). Furthermore, because
(7) 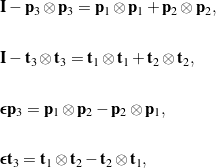
we can express the tensor ![]() entirely in terms of the axis of rotation
entirely in terms of the axis of rotation ![]() and the angle of rotation
and the angle of rotation ![]() :
:
(8) ![]()
or, equivalently,
(9) ![]()
As we shall see later, these equivalent representations naturally lead to the general form of a tensor that represents a rotation about an arbitrary axis through an arbitrary angle of rotation. As with the matrix representation of this simple rotation, the rotation tensor ![]() is a proper-orthogonal tensor because it has a determinant of one and its inverse is its transpose:
is a proper-orthogonal tensor because it has a determinant of one and its inverse is its transpose: ![]() and
and ![]() . Differentiating (5), we find that
. Differentiating (5), we find that
(10) ![]()
where we have used the fact that ![]() are constant vectors. Some straightforward computations involving (6) reveal that
are constant vectors. Some straightforward computations involving (6) reveal that
(11) ![]()
and
(12) ![Rendered by QuickLaTeX.com \begin{eqnarray*} \dot{\bf R} {\bf R}^T \!\!\!\!\! &=& \!\!\!\!\! \dot{\theta} \left( - {\bf p}_1\otimes{\bf p}_2 + {\bf p}_2\otimes{\bf p}_1\right) \\[0.10in] &=& \!\!\!\!\! \dot{\theta} \left( - {\bf t}_1\otimes{\bf t}_2 + {\bf t}_2\otimes{\bf t}_1\right). \end{eqnarray*}](https://rotations.berkeley.edu/wp-content/ql-cache/quicklatex.com-f275b5244513f41cff25a2f531e56609_l3.png)
With the help of these results, we conclude from (10) that
(13) ![]()
As expected, this result is in agreement with (4). Expression (13) implies that the vector ![]() is the axial vector of the skew-symmetric tensor
is the axial vector of the skew-symmetric tensor ![]() .
.
Notes
- For those unfamiliar with tensor notation, a review of tensors is available in the background section on linear algebra.